深度学习小记(一)

本部分内容源自这本书的第一章。和学编程语言的第一课是 “Hello world” 一样，我们来讨论一个经典而有挑战性的问题：手写数字识别。我们先从一个函数说起……

Part 01：阈值连续的神经元

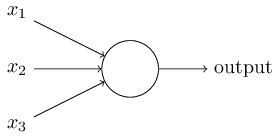
你知道函数吗，对于给定的输入向量，它会给出输出向量。函数时特别有用的数学工具，比如下面这个数学问题：

假设你想去看MyGO的演唱会，你权衡三个因素做决定。

1. 当天天气好坏。（比较重要）
2. 是否有同好一起去。（特别重要）
3. 附近交通是否方便。（不太重要）

可以设计这样一个函数 ，其中 作为权重反映了因素 的影响程度。最后根据值是否达到阈值做出判断即可。

我们简单利用线代知识就可以把这个公式写着这个形式：。不同之处在于这里的 都不再是数字，而是矩阵。

这就是感知器（perceptron）的原理。

感知器接收一组输入，若加权求和后超过阈值，输出 1。

---

然而这个函数是不完美的，由于 check（阈值判断） 的存在，这个函数是不连续 的，也就是对权重的的一个微小的调整可能使得输出发生跳变，为此必须引入连续的 check 函数（激活函数），比如 ReLU：。

把感知器的 check 换成 ReLU 函数，这就是 ReLU 神经元 (ReLU neurons) 的原理。

---

Part 02：分层连接的前馈网

人脑有近千亿（）个神经元，它们经由突触联接在一起，传递电信号，这是脑功能的重要机理。为了模拟这一功能，把神经元按层分类链接在一起，这就得到了前馈神经网络（feed forward network）。

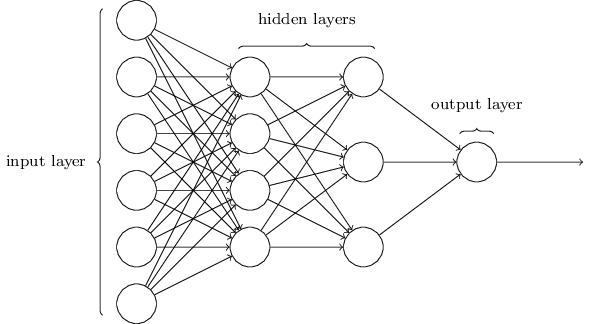
除了输入层和输出层外，我们把中间的其他神经元层称之为隐含层（hidden layer），隐含层的设计是一门艺术，它的加入为神经网络加入了相当多的权重参数，而这就是神经网络为什么有效的关键。

在这一过程中，每一个神经元都经历了大量的运算，为了简化表达，我们使用线代知识把输出升维成矩阵，就得到了前向传播公式：。

至此，从函数到神经网络的路就走完了，接下来的目的就是为了找到未知参数 。

Part 03：最值偏差的决策点

从神经网络抽离出来，我们重新来审视函数 。在小学二年级的时候我们就学过估计回归直线的“最小二乘法”，那是怎么做的？

最小二乘法：对于给定的估计点，找到合适的 k,b，使得估计直线上的点与实际点的函数值误差平方和最小。

参照这个方法，我们回到神经网络中来：

1. 神经网络本身就是一个复杂的函数，抽象其为
2. 参照“给定的估计点”，预先整理一些数据集，其中包含测试输入 与其期望输出 。
3. 参照“误差平方和”，设计成本函数, 这个成本函数叫做均方误差（MSE），当然还有很多其他的成本函数，之后介绍。
4. 参照“最小二乘法”的思想，转换目标：将 最小化。

怎么最小化一个函数？沿着负梯度方向函数值下降最快：

梯度下降的思想是：随机选取起始点，每次向负梯度方向移动一小步，最后会稳定于一个极小值。，其中移动的步长因子 称为学习率。

---

至于如何穿过种种函数的嵌套求 ，我们将在下一部分探讨。然而有一个值得提出的问题，就目前的均方误差函数而言，为了计算它的梯度，我们要对每一个样本 求梯度，然后求和取均值：, 这使得求梯度于样本数量 挂钩，会严重减低学习速度。因此就有了“随机梯度下降法”。

随机梯度下降通过随机选择一小批随机选择的训练输入来实现，通过计算随机选择的小部分训练输入的 来估计 的梯度，从而加快学习过程。

Part 04：逆向漫游的导数链

我们来简单回顾一下到目前为止的知识，下面是一个十分简单的例子：

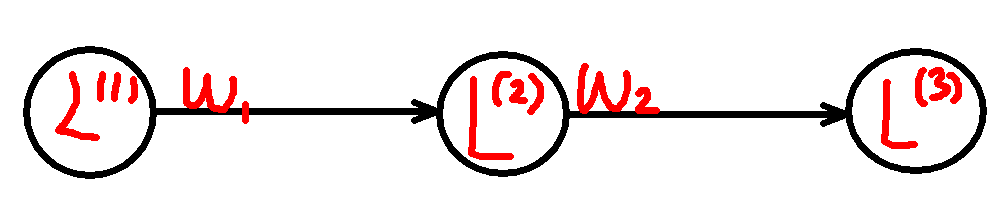
有前向传播公式：, （ 表示激活函数）

定义损失函数

唯一剩下的问题的是如何求梯度，具体地说就是求损失函数 对各个 的偏导。链式法则是解决问题的关键，我们先来画一个变量关系图。

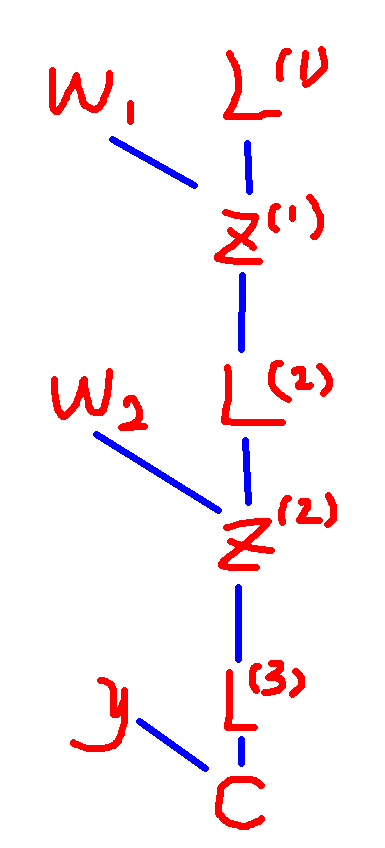
Q1：利用链式法则，如何求得？

A：，观察我们写的前向传播公式不难看出拆开的三个量都是已知的。

Q2：利用链式法则，如何求得？

A：同理，但值得注意的是和共享了这一运算。

Q3：利用链式法则，如何求得？

A：不难看出这是一个递归的过程，只要把从 到 的过程套用到从 到 上即可。

从上面的问题不难看出，这一个求梯度的过程就是一个递归的过程，在这个过程中各层之间的值，权重之间的关系是形式一致的。

回过头来看我们定义的中间变量 ，在求导过程中它起到中间枢纽的作用，我们将在之后的代码中更深入的理解这层意义，另外，我们也可以看到 与 在这个运算中有着一致的生态位，在这个意义上我们可以把 也视为误差，准确的说我们把 叫做 Delta误差。

这个从误差 向前求导数的方法就是反向传播。通过这个方法可以求得 的梯度。

虽然这个过程目前看起来很流畅，但是如果你试着将单变量拓展到矩阵时，求导的计算一下子就复杂了，这点详细解释比较晦涩我们按下不表，只谈几点转换时的几个注意事项：

• 梯度流动方向：始终与前向传播的计算图方向相反
• 维度匹配法则：
  输出梯度维度 = 前向传播输入维度
  输入梯度维度 = 前向传播输出维度
• Hadamard积保持维度：
  （特别注意这里的转置！）

参数类型	梯度计算	维度说明
权重矩阵		(当前层维度 × 前层维度)
偏置向量		保持当前层维度

简单来说，记住 和 要加转置！

---

我们在这篇文章的最后来回顾一下概念吧！

1. 输入向量

   • 符号：
   • 定义：输入特征集合，如MyGO演唱会例子中的天气、同好、交通
   • 维度：（特征数量）

2. 权重向量

   • 符号：
   • 定义：对应输入特征的重要性系数
   • 作用：加权求和时放大/缩小输入信号

3. 阈值（偏置）

   • 符号：
   • 定义：神经元激活的临界值
   • 公式：

4. 激活函数

   • 示例：ReLU 函数
   • 公式：
   • 作用：引入非线性表达能力

5. 前向传播公式

   • 符号：
   • 说明：
     • ：第 层输出
     • ：权重矩阵
     • ：偏置向量

6. 成本函数（MSE）

   • 公式：
   • 变量说明：
     • ：真实标签
     • ：模型预测值
     • ：样本数量

7. 梯度下降更新规则

   • 公式：
   • 参数说明：
     • ：学习率（步长）
     • ：成本函数梯度

8. 随机梯度下降（SGD）

   • 特点：
     • 使用小批量样本计算梯度
     • 公式：

9. 链式法则应用

   • 示例：
     
   • 说明：通过反向传播逐层计算参数梯度

10. Delta误差

    • 符号：
    • 定义：
      第 层误差项，表示损失对当前层输出的敏感度
    • 计算公式：
      

至此，原理暂时告一段落，是时候写点代码了，我们下个文章见！

---

感谢你看到这里，今天要放的歌是…《我没有歌能给你听》

我没有歌能给你听

但我还没有歌给你听

对不起　至少现在还不行

城市闪烁　我不知在怕什么

有个声音 在 拉扯另一个

我没有歌能给你听

对不起　连失望的人　也渐渐地消失了踪影

城市闪烁　我不能总是躲着

我想请你告诉我

当我再一次 对你开口

如果有天再一次 对你开口

是否你会再一次 听允许我

是否你会再一次 听我唱歌

我的琴弦再一次 为你铭刻

让时光再一次 为你流动

一些 过去曾 流浪的 人 风 一些景色

我的悲伤 流淌 你的快乐

感谢你的阅读~